
Two supplementary angles form a straight angle and two complementary angles form a right angle. The supplementary angles are those whose sum is 180 degrees while the sum of two complementary angles is 90 degrees. What is the Difference Between Supplementary and Complementary Angles? Hence, if X and Y are complementary, this implies that, ∠X + ∠Y = 90°. The sum of two complementary angles is always 90 degrees. What is the Sum of Two Complementary Angles? For example, the complement of 40° is 90° - 40° = 50°. Thus, the complement of an angle is obtained by subtracting it from 90. If the sum of two angles is 90 degrees, then we say that they are complementary. If ∠A and ∠B are complementary angles, it implies that: Two complementary angles always add up to 90 degrees. If ∠1 and ∠2 are complementary angles, then ∠1 + ∠2 = 90°. In geometry, two angles are said to be complementary angles if they add up to 90 degrees. Complementary and Supplementary Angles WorksheetsįAQs on Complementary Angles What does Complementary Angles Mean?.Now subtract '∠POQ' from both sides, ∠AOP = ∠QOR.Ĭheck out the following important articles to know more about complementary angles in math.From the above two equations, we can say that "∠POQ + ∠AOP = ∠POQ + ∠QOR".Now as per the definition of complementary angles, ∠POQ + ∠AOP = 90° and ∠POQ + ∠QOR = 90°.Let us assume that ∠POQ is complementary to ∠AOP and ∠QOR.Consider the following figure and prove the complementary angle theorem. We know that complementary angles exist in pairs and sum up to 90 degrees. The complementary angle theorem states, " If two angles are complementary to the same angle, then they are congruent to each other". Let's study the complementary angles theorem with its proof. Each of the complement angles is acute and positive. "C" is for "Complementary" and "C" is for "Corner." Hence, you can remember that two "Complementary" angles when put together form a "Corner (right)" angle."S" is for "Supplementary" and "S" is for "Straight." Hence, you can remember that two "Supplementary" angles when put together form a "Straight" angle.Here is a short trick for you to understand complementary angles vs supplementary angles. They can be joined together to form a right angle. They can be joined together to form a straight angle. The complement of an angle x° is (90 - x)°.
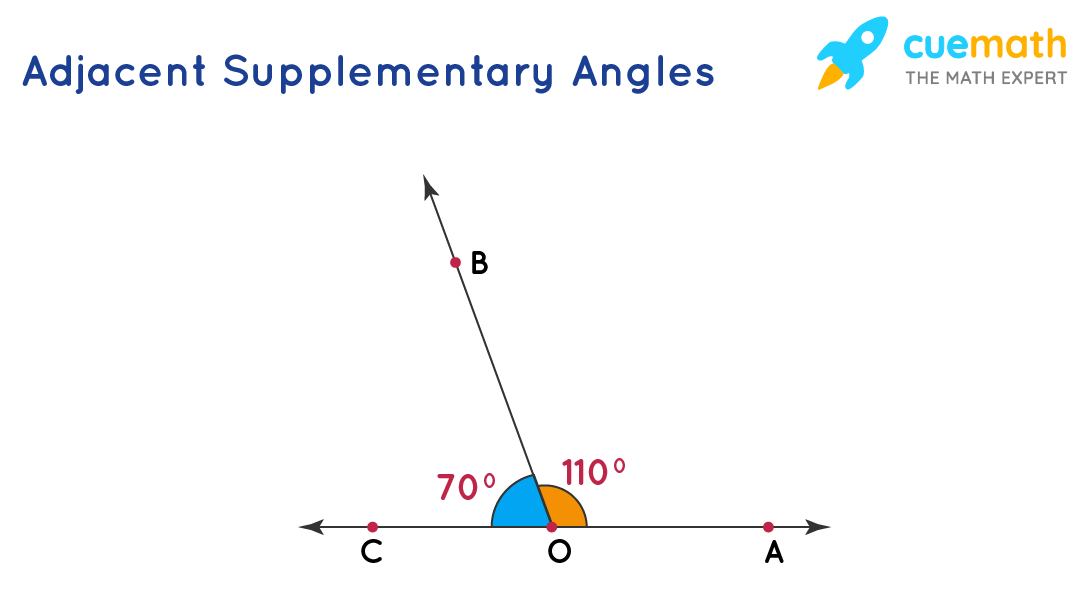
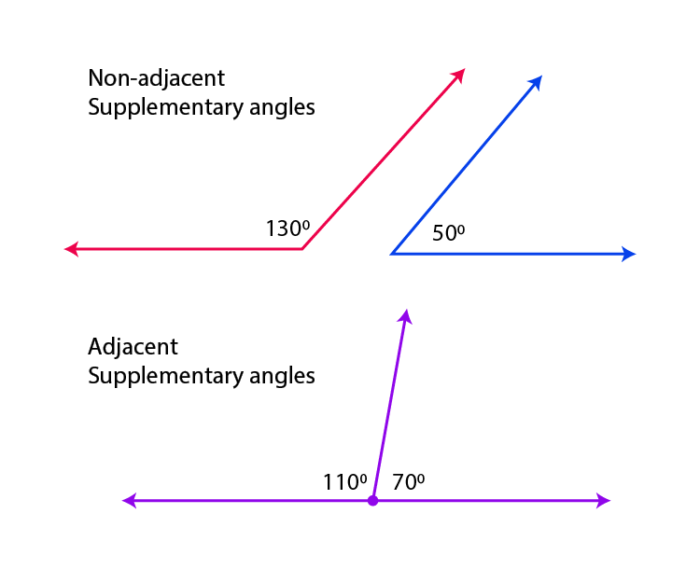
The difference between complementary angles and supplementary angles are given in the table below: Supplementary AnglesĪ pair of angles are said to be supplementary if their sum is 180 degrees.Ī pair of angles are said to be complementary if their sum is 90 degrees. When complementary angles can be considered as two parts of a right angle, the supplementary angles are the two parts of a straight angle or a 180-degree angle. They can either be adjacent or non-adjacent. The complementary and supplementary angles are those that add up to 90 degrees and 180 degrees respectively. When non-adjacent complementary angles are put together, they form a right angle.Ĭomplementary Angles and Supplementary Angles Thus, these two angles are non-adjacent complementary angles. Also, they add up to 90 degrees that is, ∠ABC + ∠PQR = 50° + 40° = 90°. In the figure given below, ∠ABC and ∠PQR are non-adjacent angles as they neither have a common vertex nor a common arm. Non-adjacent Complementary Angles: Two complementary angles that are NOT adjacent are said to be non-adjacent complementary angles. Thus, these two angles are adjacent complementary angles. They also add up to 90 degrees, that is ∠COB + ∠AOB = 70° + 20° = 90°. In the figure given below, ∠COB and ∠AOB are adjacent angles as they have a common vertex "O" and a common arm "OB". There are two types of complementary angles in geometry as given below:Īdjacent Complementary Angles: Two complementary angles with a common vertex and a common arm are called adjacent complementary angles. If the sum of two angles is equal to the measurement of a right angle then the pair of angles is known as the complementary angle.


 0 kommentar(er)
0 kommentar(er)
